rougier/fractal-dimension.py

delton137 · 2020-11-06T16:43:12Z

Here is the code I'm using :
https://repl.it/repls/AlarmingHarmlessScience

Thank you for your help with this!!

rougier · 2020-11-10T20:23:56Z

Looking at https://en.wikipedia.org/wiki/Minkowski%E2%80%93Bouligand_dimension, I think I may have computer the dimension of the border and not the actual shape because I filtered out the full boxes. This may explain why the result is 1.

delton137 · 2020-11-10T20:50:08Z

If I run on a rectangle, I get something around 0.55. I think it should be pretty close to either 1 or 2 depending how you did it. To be honest I haven't had time to review your code in depth. I am actually analyzing a 3D shape and using fractal dimension as a measure of surface irregularity, so I'm using a 3D fractal dimension code I found elsewhere for that. So this is not a high priority for me. However I thought it might be worth looking at the fractal dimension for 2D slices of the object as well.

akshahi17 · 2021-01-19T22:08:56Z

I am getting this error message when executing this programme in PyCharm.
1)"AttributeError: module 'scipy.misc' has no attribute 'imread'"
2) "AttributeError: module 'scipy' has no attribute 'misc'"

rougier · 2021-01-20T08:32:20Z

@akshahi17 Probably the imread function has been deprecated in scipy. You cn now use the imageio library instead.

jankaWIS · 2021-03-16T16:02:05Z

Hi, I was testing it on some fractals with defined dimensions, below is my code. The problem is that it's far from the dimensions and even for the same fractal in a different rotation (Sherpinski), it is not giving the same values (which I believe should, this should be independent of rotation). Where is the problem?

Also, I believe that it should go to squares 2x2, that is:
sizes = 2**np.arange(n, 2, -1) should become sizes = 2**np.arange(n, 0, -1).

Source:
https://en.wikipedia.org/wiki/Sierpi%C5%84ski_carpet

https://en.wikipedia.org/wiki/Koch_snowflake

# -----------------------------------------------------------------------------
# From https://en.wikipedia.org/wiki/Minkowski–Bouligand_dimension:
#
# In fractal geometry, the Minkowski–Bouligand dimension, also known as
# Minkowski dimension or box-counting dimension, is a way of determining the
# fractal dimension of a set S in a Euclidean space Rn, or more generally in a
# metric space (X, d).
# -----------------------------------------------------------------------------

import numpy as np
import matplotlib.pyplot as plt

def fractal_dimension(Z, threshold=0.9):

    # Only for 2d image
    assert(len(Z.shape) == 2)

    # From https://github.com/rougier/numpy-100 (#87)
    def boxcount(Z, k):
        S = np.add.reduceat(
            np.add.reduceat(Z, np.arange(0, Z.shape[0], k), axis=0),
                               np.arange(0, Z.shape[1], k), axis=1)

        # We count non-empty (0) and non-full boxes (k*k)
        return len(np.where((S > 0) & (S < k*k))[0])


    # Transform Z into a binary array
    Z = (Z < threshold)

    # Minimal dimension of image
    p = min(Z.shape)

    # Greatest power of 2 less than or equal to p
    n = 2**np.floor(np.log(p)/np.log(2))

    # Extract the exponent
    n = int(np.log(n)/np.log(2))

    # Build successive box sizes (from 2**n down to 2**1)
    sizes = 2**np.arange(n, 1, -1)

    # Actual box counting with decreasing size
    counts = []
    for size in sizes:
        counts.append(boxcount(Z, size))

    # Fit the successive log(sizes) with log (counts)
    coeffs = np.polyfit(np.log(sizes), np.log(counts), 1)
    return -coeffs[0]

special = [
    'https://upload.wikimedia.org/wikipedia/commons/thumb/7/7c/Peano_Sierpinski_carpet_4.svg/440px-Peano_Sierpinski_carpet_4.svg.png',
    'https://upload.wikimedia.org/wikipedia/commons/thumb/3/3b/Quadratic_Koch_2.svg/2880px-Quadratic_Koch_2.svg.png',
    'https://upload.wikimedia.org/wikipedia/commons/thumb/5/55/Quadratic_Koch.svg/300px-Quadratic_Koch.svg.png'
]
images = [
    'https://upload.wikimedia.org/wikipedia/commons/thumb/7/7c/Peano_Sierpinski_carpet_4.svg/440px-Peano_Sierpinski_carpet_4.svg.png',
    'https://upload.wikimedia.org/wikipedia/commons/thumb/b/b7/Sierpinski_carpet_3.svg/244px-Sierpinski_carpet_3.svg.png',
    'https://upload.wikimedia.org/wikipedia/commons/f/f0/Flocke.PNG',
    'https://upload.wikimedia.org/wikipedia/commons/thumb/3/3b/Quadratic_Koch_2.svg/2880px-Quadratic_Koch_2.svg.png',
    'https://upload.wikimedia.org/wikipedia/commons/thumb/5/55/Quadratic_Koch.svg/300px-Quadratic_Koch.svg.png'
]

dimensions = [(np.log(3)/np.log(2)), (np.log(3)/np.log(2)), (np.log(4)/np.log(3)), 1.46, 1.5]


for dim, im in zip(dimensions, images):
    # load im
    x = plt.imread(im)
    if im in special:
        print("Minkowski–Bouligand dimension (computed): ", fractal_dimension(x[:,:,3]))
        print("theoretical:        ", dim)
        plt.imshow(x[:,:,3])
        plt.show()
        
    else:
        print("Minkowski–Bouligand dimension (computed): ", fractal_dimension(x[:,:,1]))
        print("theoretical:        ", dim)
        plt.imshow(x[:,:,1])        
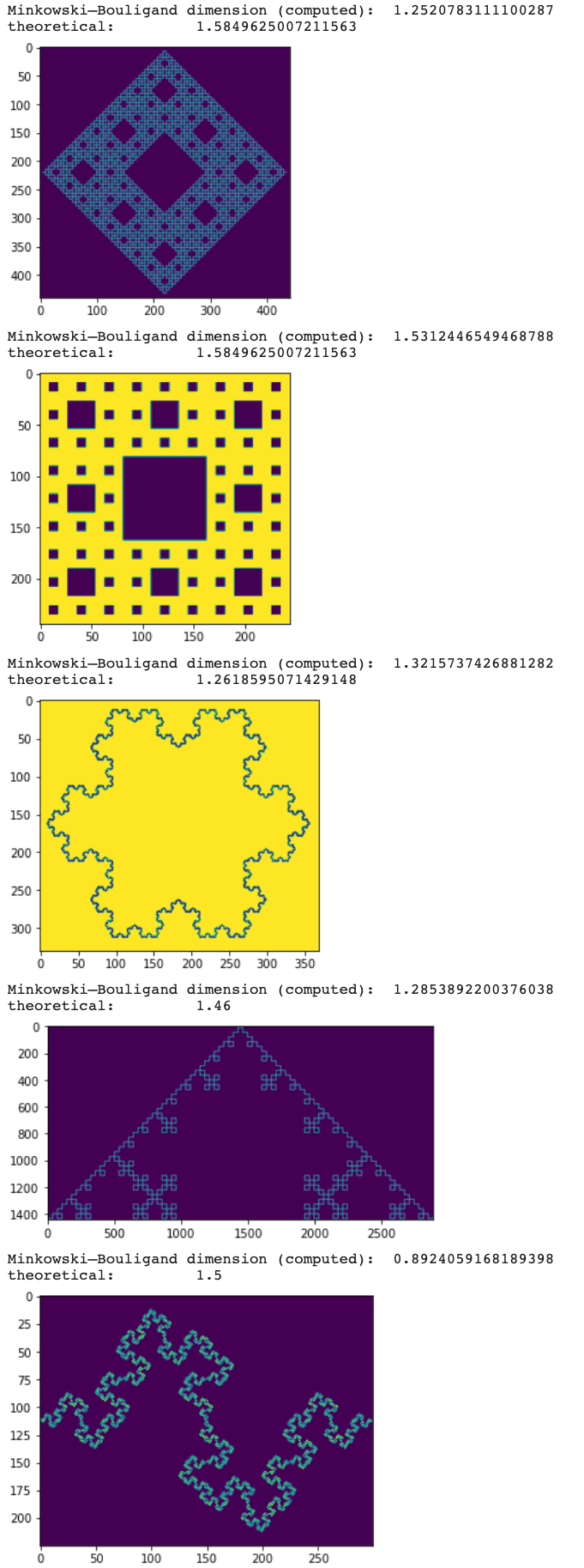
        plt.show()

and the result:
Minkowski–Bouligand dimension (computed): 1.2520783111100287
theoretical: 1.5849625007211563

Minkowski–Bouligand dimension (computed): 1.5312446549468788
theoretical: 1.5849625007211563

Minkowski–Bouligand dimension (computed): 1.3215737426881282
theoretical: 1.2618595071429148

Minkowski–Bouligand dimension (computed): 1.2853892200376038
theoretical: 1.46

Minkowski–Bouligand dimension (computed): 0.8924059168189398
theoretical: 1.5

rougier · 2021-03-17T07:52:23Z

I'm not sure but the images seems to be a bit noisy which might impact the computation. Can you try to make black and white (for example I = I > 0.5 and check if the result is the same? If this is the case, this means we need some threshold value when deciding if a box is empty or not.

jankaWIS · 2021-03-17T08:27:59Z

Except for the first and last, they are all binary (ie B&W). I have tried and you were right, @rougier, about those, setting the threshold to 0.2 works on them.

What about this note?

Also, I believe that it should go to squares 2x2, that is:
sizes = 2**np.arange(n, 2, -1) should become sizes = 2**np.arange(n, 0, -1).

I am curious because you used to have it that way (at least that is what I see in the history) but you have a discrepancy in the note and in the code. Your code says:

2**np.arange(n, 1, -1) # eg for n=4  you get array([16,  8,  4])

but the comment says
Build successive box sizes (from 2**n down to 2**1) which suggest this code:

2**np.arange(n, 0, -1) # eg for n=4  you get array([16,  8,  4,  2])

And that I believe is the correct code.

Code

import numpy as np
import matplotlib.pyplot as plt

def fractal_dimension(Z, threshold=0.9):

    # Only for 2d image
    assert(len(Z.shape) == 2)

    # From https://github.com/rougier/numpy-100 (#87)
    def boxcount(Z, k):
        S = np.add.reduceat(
            np.add.reduceat(Z, np.arange(0, Z.shape[0], k), axis=0),
                               np.arange(0, Z.shape[1], k), axis=1)

        # We count non-empty (0) and non-full boxes (k*k)
        return len(np.where((S > 0) & (S < k*k))[0])


    # Transform Z into a binary array
    Z = (Z < threshold)
    plt.imshow(Z)
    plt.show()

    # Minimal dimension of image
    p = min(Z.shape)

    # Greatest power of 2 less than or equal to p
    n = 2**np.floor(np.log(p)/np.log(2))

    # Extract the exponent
    n = int(np.log(n)/np.log(2))

    # Build successive box sizes (from 2**n down to 2**1)
    sizes = 2**np.arange(n, 1, -1)

    # Actual box counting with decreasing size
    counts = []
    for size in sizes:
        counts.append(boxcount(Z, size))

    # Fit the successive log(sizes) with log (counts)
    coeffs = np.polyfit(np.log(sizes), np.log(counts), 1)
    return -coeffs[0]

special = [
    'https://upload.wikimedia.org/wikipedia/commons/thumb/7/7c/Peano_Sierpinski_carpet_4.svg/440px-Peano_Sierpinski_carpet_4.svg.png',
    'https://upload.wikimedia.org/wikipedia/commons/thumb/3/3b/Quadratic_Koch_2.svg/2880px-Quadratic_Koch_2.svg.png',
    'https://upload.wikimedia.org/wikipedia/commons/thumb/5/55/Quadratic_Koch.svg/300px-Quadratic_Koch.svg.png'
]
images = [
    'https://upload.wikimedia.org/wikipedia/commons/thumb/7/7c/Peano_Sierpinski_carpet_4.svg/440px-Peano_Sierpinski_carpet_4.svg.png',
    'https://upload.wikimedia.org/wikipedia/commons/thumb/b/b7/Sierpinski_carpet_3.svg/244px-Sierpinski_carpet_3.svg.png',
    'https://upload.wikimedia.org/wikipedia/commons/f/f0/Flocke.PNG',
    'https://upload.wikimedia.org/wikipedia/commons/thumb/3/3b/Quadratic_Koch_2.svg/2880px-Quadratic_Koch_2.svg.png',
    'https://upload.wikimedia.org/wikipedia/commons/thumb/5/55/Quadratic_Koch.svg/300px-Quadratic_Koch.svg.png'
]

dimensions = [(np.log(3)/np.log(2)), (np.log(3)/np.log(2)), (np.log(4)/np.log(3)), 1.46, 1.5]


for dim, im in zip(dimensions, images):
    # load im
    x = plt.imread(im)
    if im in special:
        print("Minkowski–Bouligand dimension (computed): ", fractal_dimension(x[:,:,3], threshold=0.2))
        print("theoretical:        ", dim)
        print(f"min {x[:,:,3].min()} and max {x[:,:,3].max()} in the array/image")
        
    else:
        print("Minkowski–Bouligand dimension (computed): ", fractal_dimension(x[:,:,1],threshold=0.2))
        print("theoretical:        ", dim)
        print(f"min {x[:,:,1].min()} and max {x[:,:,1].max()} in the array/image")

jankaWIS · 2021-03-17T08:32:59Z

I am getting this error message when executing this programme in PyCharm.
1)"AttributeError: module 'scipy.misc' has no attribute 'imread'"
2) "AttributeError: module 'scipy' has no attribute 'misc'"

@akshahi17 check this answer https://stackoverflow.com/questions/15345790/scipy-misc-module-has-no-attribute-imread
the function has been deprecated so you can either downgrade (not recommended) or use what @rougier recommended (imageio) or what I'm using, imread in matplotlib.pyplot.

barbaroo · 2022-01-24T17:46:46Z

Hi! I found this code very useful and I would like to cite it in my paper. Is there a correct way to cite this? Please help! I have to submit soon!

rougier · 2022-01-31T17:43:47Z

Glad the code is useful but I'm afraid there there's no proper way to cite a it. Maybe as a misc bibitem with the relevant url/author.

antoni27 · 2022-04-09T16:23:10Z

hello

sorry, can anyone tell me how to change the data that I want to get from the link to my laptop data?
I want to try to extract features of an iris

jankaWIS · 2022-04-17T08:20:13Z

Hi @antoni27, I am not really sure what data you have and how you want to use it but simply changing the path in line 52 of the original code to link to another image should be enough.

antoni27 · 2022-05-09T17:34:38Z

thanks, @jankaWIS
and sorry if I ask again is the 52 line is
images = [
'https://upload.wikimedia.org/wikipedia/commons/thumb/7/7c/Peano_Sierpinski_carpet_4.svg/440px-Peano_Sierpinski_carpet_4.svg.png',
'https://upload.wikimedia.org/wikipedia/commons/thumb/b/b7/Sierpinski_carpet_3.svg/244px-Sierpinski_carpet_3.svg.png',
'https://upload.wikimedia.org/wikipedia/commons/f/f0/Flocke.PNG',
'https://upload.wikimedia.org/wikipedia/commons/thumb/3/3b/Quadratic_Koch_2.svg/2880px-Quadratic_Koch_2.svg.png',
'https://upload.wikimedia.org/wikipedia/commons/thumb/5/55/Quadratic_Koch.svg/300px-Quadratic_Koch.svg.png'
]
?

sorry I using the jupyter notebook so not to know about the number

zyzhoux · 2022-06-21T02:04:55Z

Why are boxes of 2x2 excluded?

VaeKnt · 2024-08-12T14:28:21Z

Hello, thank you very much for this function. I am finding it very useful in my study of fractals.

However, I drew a jagged line and tried to compute the fractal dimension

Using this code, I get a dimension of around 0.94 which is clearly wrong as it is < 1.

Why am I getting such a number?

Additionally, with other free fractal analysis software, I get a dimension of around 1.088

This is the line for reference

delton137 · 2024-08-12T14:34:01Z

FWIW the calculation is approximate.. also look at my comment above, there might still be a subtle issue with this code.

VaeKnt · 2024-08-13T10:35:01Z

Hi delton137!

I used another simple line that I generated, and then with altering the number of boxes, and then after iterating and computing the mean, I believe I got a better estimate. For this other curve, the box-count dimension was 1.06 ish. And it was well within the 95% CI range when I compared it to the FD from the one measured by the software.

I think I hopefully solved my own problem. I came across some papers re: optimal sizes of boxes. I will need to see how to implement that!

Also, I saw that you are also working in medical imaging. It is very inspiring to see interest in fractals and medical imaging. I am but a mere medical student currently, I hope to see a lot more fractals in the future, and a lot more collaboration!

rougier/fractal-dimension.py

delton137 commented Nov 6, 2020

rougier commented Nov 10, 2020

delton137 commented Nov 10, 2020

akshahi17 commented Jan 19, 2021

rougier commented Jan 20, 2021

jankaWIS commented Mar 16, 2021 •

edited

Loading

rougier commented Mar 17, 2021

jankaWIS commented Mar 17, 2021 •

edited

Loading

jankaWIS commented Mar 17, 2021

barbaroo commented Jan 24, 2022

rougier commented Jan 31, 2022

antoni27 commented Apr 9, 2022 •

edited

Loading

jankaWIS commented Apr 17, 2022 •

edited

Loading

antoni27 commented May 9, 2022 •

edited

Loading

zyzhoux commented Jun 21, 2022

VaeKnt commented Aug 12, 2024

delton137 commented Aug 12, 2024

VaeKnt commented Aug 13, 2024

	# -----------------------------------------------------------------------------
	# From https://en.wikipedia.org/wiki/Minkowski–Bouligand_dimension:
	#
	# In fractal geometry, the Minkowski–Bouligand dimension, also known as
	# Minkowski dimension or box-counting dimension, is a way of determining the
	# fractal dimension of a set S in a Euclidean space Rn, or more generally in a
	# metric space (X, d).
	# -----------------------------------------------------------------------------
	import scipy.misc
	import numpy as np


	def fractal_dimension(Z, threshold=0.9):

	# Only for 2d image
	assert(len(Z.shape) == 2)

	# From https://github.com/rougier/numpy-100 (#87)
	def boxcount(Z, k):
	S = np.add.reduceat(
	np.add.reduceat(Z, np.arange(0, Z.shape[0], k), axis=0),
	np.arange(0, Z.shape[1], k), axis=1)

	# We count non-empty (0) and non-full boxes (k*k)
	return len(np.where((S > 0) & (S < k*k))[0])


	# Transform Z into a binary array
	Z = (Z < threshold)

	# Minimal dimension of image
	p = min(Z.shape)

	# Greatest power of 2 less than or equal to p
	n = 2**np.floor(np.log(p)/np.log(2))

	# Extract the exponent
	n = int(np.log(n)/np.log(2))

	# Build successive box sizes (from 2n down to 21)
	sizes = 2**np.arange(n, 1, -1)

	# Actual box counting with decreasing size
	counts = []
	for size in sizes:
	counts.append(boxcount(Z, size))

	# Fit the successive log(sizes) with log (counts)
	coeffs = np.polyfit(np.log(sizes), np.log(counts), 1)
	return -coeffs[0]

	I = scipy.misc.imread("sierpinski.png")/256.0
	print("Minkowski–Bouligand dimension (computed): ", fractal_dimension(I))
	print("Haussdorf dimension (theoretical): ", (np.log(3)/np.log(2)))

rougier/fractal-dimension.py

delton137 commented Nov 6, 2020

rougier commented Nov 10, 2020

delton137 commented Nov 10, 2020

akshahi17 commented Jan 19, 2021

rougier commented Jan 20, 2021

jankaWIS commented Mar 16, 2021 • edited Loading

rougier commented Mar 17, 2021

jankaWIS commented Mar 17, 2021 • edited Loading

jankaWIS commented Mar 17, 2021

barbaroo commented Jan 24, 2022

rougier commented Jan 31, 2022

antoni27 commented Apr 9, 2022 • edited Loading

jankaWIS commented Apr 17, 2022 • edited Loading

antoni27 commented May 9, 2022 • edited Loading

zyzhoux commented Jun 21, 2022

VaeKnt commented Aug 12, 2024

delton137 commented Aug 12, 2024

VaeKnt commented Aug 13, 2024

jankaWIS commented Mar 16, 2021 •

edited

Loading

jankaWIS commented Mar 17, 2021 •

edited

Loading

antoni27 commented Apr 9, 2022 •

edited

Loading

jankaWIS commented Apr 17, 2022 •

edited

Loading

antoni27 commented May 9, 2022 •

edited

Loading